|
|
Vol.
33 No. 2
March-April 2011
Atomic Weights: No Longer Constants of Nature
by Tyler B. Coplen and Norman E. Holden
Many of us were taught that the standard atomic weights we found in the back of our chemistry textbooks or on the Periodic Table of the Chemical Elements hanging on the wall of our chemistry classroom are constants of nature. This was common knowledge for more than a century and a half, but not anymore. The following text explains how advances in chemical instrumentation and isotopic analysis have changed the way we view atomic weights and why they are no longer constants of nature.
 |
|
Atomic Weight
The concept of atomic weights goes back to the time of John Dalton at the beginning of the 19th century. Much of chemistry in the first half of that century involved the measurement and analysis of atomic weights. Many scientists, most notably Dmitri Mendeleev, analyzed and divided the atomic weights of the elements into triads, octaves, and spirals, based on similarities of the chemical and physical properties of these elements. Mendeleev provided a periodic table along with predictions of new elements to fill gaps in his table, and these elements subsequently were discovered. In 1882, Frank W. Clarke recommended atomic-weight values for use in science, industry, and trade.1 The American Chemical Society appointed Clarke as a one-man committee to issue atomic-weight tables annually. Groups in other countries created committees with a similar purpose. The values of the atomic-weight tables of these committees often differed, however, leading the German Atomic Weights Commission to call for an international commission to determine atomic weights. The first report (1901) of the International Commission on Atomic Weights (ICAW) was published as a flyleaf in the first issue of the Chemische Berichte in January 1902.2 In 1913, the Commission became part of the International Association of Chemical Societies (IACS). Although IACS was dissolved following World War I, the Commission continued to publish updated tables of atomic weights each year until 1921–1922. In 1919, the International Union of Pure and Applied Chemistry (IUPAC) was created as the chemical section of the International Research Council. An atomic-weight report from a new Commission, under IUPAC auspices, was first prepared in 1925. Since that time, ICAW or its successors within IUPAC, hereafter termed the Commission, took over the careful evaluation and dissemination of atomic-weight values, which continued to be considered “constants of nature.”
Isotopes
A constant of nature, such as the Faraday constant
[96 485.3399(24) C mol–1], typically is known to better than 1 part in a million parts. IUPAC’s Periodic Table3 lists a value of 10.811(7) for boron. If standard atomic weights are constants of nature, why are the values not published with greater accuracy? The answer, of course, is that the atomic weight of an element depends upon the source of the material and upon its number of stable isotopes, where isotopes are atoms of the same element having different mass numbers. At the start of the twentieth century, radioactive elements were discovered. Fredrick Soddy showed the chemical identity of meso-thorium (228Ra) and radium (226Ra).4 He concluded that these chemical elements had different radioactive properties and different atomic weights, but the same chemical properties and so should occupy the same positions in the Periodic Table of the Elements. He coined the word “isotope” (Greek: “in the same place”) to account for radioactive species.5 An event that profoundly affected atomic weights was the discovery by John (J.J.) Thomson6 in 1912 that the element neon was made up of two stable isotopes, 20Ne and 22Ne. (21Ne was discovered later.) With the discovery of stable isotopes and the use of mass spectrographs to measure the isotopic composition of chemical elements, it was realized that the masses of the individual stable isotopes and their isotopic-abundance values (mole fractions) could provide an alternative method for estimating an element’s atomic weight. With technical improvements to mass spectrometers, the accuracy of this method began to exceed that of chemical determinations of atomic weight. Over the last half of the 20th century, almost every new recommended atomic-weight value was based on mass spectrometric measurements.
Variations in Abundances of Isotopes and Atomic Weights
In 1908, the atomic weight of “common” lead (from a nonradioactive source material) was measured to be 207.2,7 while a 1914 measurement8 of lead from a thorium silicate mineral had an atomic weight of 208.4. A low value of 206.4 was measured for the atomic weight of lead in uranium samples in 1914.9 Differences in lead atomic-weight values were considered to be an exceptional case that was attributed to lead isotopes being products of the natural radioactive decay chains. However, in 1936, Malcolm Dole10 reported the variation of oxygen’s atomic-weight value in air and in water, because of variations in abundances of its stable isotopes. In 1939, Alfred O.C. Nier11 reported on the 5 percent variation in the isotopic composition of carbon. It was becoming clear that atomic weights might not be constants of nature. At the Commission’s meeting in 1951, it was recognized that the isotopic-abundance variation of sulfur impacted the internationally accepted value of an atomic weight.12 In order to indicate the span of values that may apply to sulfur from different natural sources, the value ± 0.003 was attached to the atomic weight of sulfur. Ranges were listed for six elements (H, B, C, O, Si, and S) due to the natural variation in their isotopic compositions, and experimental uncertainties were added for an additional five elements (Cl, Cr, Fe, Br, and Ag) in the 1961 report of the Commission.13 In the 1969 report of the Commission,14 uncertainties were added for all atomic-weight values for the first time. IUPAC had now added to its responsibilities the careful evaluation and dissemination of atomic-weight uncertainties, derived from critically assessed published information. Also in the 1969 report, the Commission acknowledged for the first time that
the discovery that most chemical elements exist in nature as isotopic mixtures, many of which are known to vary in composition, makes it necessary to modify the historical concept of atomic weights as constants of nature. Even though [stable] isotopes have not been observed in nature for some elements (currently 21 in number), it appears more logical to consider that isotopic mixtures represent the normal rather than the exceptional state of an element. The Commission considers that this attitude will promote an awareness that uncertainties in the values given in the International Table are no longer, as in earlier times, to be regarded as resulting only from errors in the measurement of the value, but that they arise from natural variations in isotopic composition. . . . To arrive at the recommended value for the atomic weight the Commission will use weighting procedures so that the value will be optimized for materials in world science, chemical technology and trade, rather than represent an estimated geochemical average.
Not all elements, though, exhibit variations in their atomic weights; some have only one stable isotope. Determination of the standard atomic weights of the 21 elements with a single stable isotope,15 such as F, Al, Na, and Au, is relatively simple because they depend only upon the atomic mass of a single stable isotope. These standard atomic weights are constants of nature, and their values are known to be better than one part in a million parts.
As a result of the growing importance of isotopic measurements for atomic weights, the Commission changed its name in 1979 to the Commission on Atomic Weights and Isotopic Abundances. The Commission decided that an atomic weight could be defined for any specified sample. For the IUPAC table of recommended values of atomic weights, the Commission stated:
Dated Tables of Standard Atomic Weights published by the Commission refer to our best knowledge of the elements in natural terrestrial sources.16
Atomic-weight distributions determined from published variations in isotopic compositions can span relatively large intervals. Figure 1 shows the variation in atomic weight as a function of mole fraction of 2H in selected hydrogen-bearing materials. The atomic weight of hydrogen in “normal” materials spans atomic-weight values from approximately 1.00785 to 1.00811,17–19 whereas the uncertainty of the atomic weight calculated from the best measurement20 of the isotopic abundance of hydrogen is about a thousand times smaller: Ar(H) = 1.007 981 75(5). By a “normal” material, the Commission means a material from a terrestrial source that satisfies the following criterion:
The material is a reasonably possible source for this element or its compounds in commerce, for industry or science; the material is not itself studied for some extraordinary anomaly and its isotopic composition has not been modified significantly in a geologically brief period.21
To determine the atomic-weight value of an element having variations in the abundances of its stable isotopes in natural materials that result in a span of atomic-weight values (e.g., H, Li, B, C, N, etc.), the Commission typically has evaluated published variations in isotopic compositions, selected an atomic weight near the median value as the standard atomic weight, and assigned an uncertainty to encompass most or all of the published atomic-weight values. For example, for hydrogen (figure 1) the Commission selected at its 1981 meeting22 a standard atomic-weight value of 1.007 94 with an uncertainty of 0.000 07. The Commission’s concern that the chemical community would have difficulty handling asymmetric uncertainties and that most computer programs would not be able to treat asymmetric uncertainties properly led the Commission always to adopt symmetric uncertainties for standard atomic-weight values, even in cases where asymmetric uncertainties were called for. This presentation method is unsatisfactory for several reasons:
- Students and others commonly misinterpret the uncertainty value of the standard atomic weight as a measurement uncertainty, and they wonder why standard atomic weights cannot be determined more accurately.
- In years following the determination of a new standard atomic weight, newly published natural variations provide atomic-weight values that commonly exceed the bounds of the newly adopted standard atomic-weight value; thus, standard atomic weights needed to be changed regularly or they did not reflect recently published scientific literature.
- The standard atomic-weight value is commonly expected by readers to reflect a Gaussian distribution, and it does not reflect satisfactorily the bimodal distribution of some elements—for example, that of boron and sulfur.17,18
- It is often difficult, or even impossible, to find a material with an atomic-weight value identical to the standard atomic weight. For example, finding a hydrogen-bearing material with an atomic weight of 1.007 94 would be a
challenge.
|
| Figure 1. Variation in atomic weight with isotopic abundance of selected hydrogen-bearing materials.17–19 Isotopic reference materials are designated by solid black circles. The previous (2007) standard atomic weight of hydrogen was 1.007 94(7). The atomic-weight uncertainty of the “best measurement” of isotopic abundance20 is approximately ±0.000 000 05, which is about 1000 times smaller than the uncertainty of the 2007 standard atomic weight.23 |
Atomic-Weight Intervals
A new presentation method for standard atomic weights of elements such as H, Li, B, C, and N was needed. At its meeting in 2009 in Vienna, the Commission decided to express the standard atomic weight of hydrogen and nine other elements in a manner that clearly indicates that the values are not constants of nature.24 The span of atomic-weight values in normal materials is termed the “interval.” The interval is used together with the symbols [a; b] to denote the set of values x for which a ≤ x ≤ b, where b > a and where a and b are the lower and upper bounds, respectively.25 Neither the upper nor lower bounds have any uncertainty associated with them; each is a considered decision by the Commission based on professional evaluation and judgment. Writing the standard atomic weight of hydrogen as [1.007 84; 1.008 11] indicates that the atomic weight in any normal material will be greater than or equal to 1.007 84 and will be less than or equal to 1.008 11. Thus, the atomic-weight interval is said to encompass atomic-weight values of all normal materials. The range of an interval is the difference between b and a—that is, b – a.25 Thus, the range of the atomic-weight interval of hydrogen is calculated as 1.008 11 – 1.007 84 = 0.000 27. The lower bound of an atomic-weight interval is determined from the lowest atomic weight determined by the Commission’s evaluations, taking into account the uncertainty of the measurement. Commonly, a mass spectrometrically determined isotope-delta measurement17,18 is the basis for the determination of the bound. In addition to the uncertainty in the isotope-delta measurement, the uncertainty in the atomic weight of the material anchoring the delta scale is also taken into account.17,18 If substance P is the normal terrestrial material having the lowest atomic weight of element E, then
lower bound = lowest Ar(E)P – U[Ar(E)]P
where U[Ar(E)]P is the combined uncertainty that incorporates the uncertainty in the measurement of the delta value of substance P and the uncertainty in relating the delta-value scale to the atomic-weight scale. For hydrogen, the substance with the lowest published, evaluated 2H abundance is hydrogen gas in a natural gas well,17,18 and for it Ar(H) = 1.007 8507, and U[Ar(H)] = 0.000 0046. Thus, the lower bound is 1.007 8461. The combined uncertainty constrains the number of significant figures in the atomic-weight value of the bound. For hydrogen, the sixth digit after the decimal point is uncertain; therefore, the value is truncated to five digits after the decimal point. For the lower bound of hydrogen, 1.007 8461 is truncated to 1.007 84. The upper bound is determined in an equivalent manner, but for an upper bound, the trailing digit is increased to ensure the atomic-weight interval encompasses the atomic-weight values of all normal materials. The lower and upper bounds are evaluated so that the number of significant digits in each is identical. If a value ends with a zero, the zero may need to be included in the value to express the required number of digits.
Elements whose 2007 atomic weights are now presented as intervals24 are shown in the following table.
| Element name |
2007 Atomic Weight23 |
2009 Atomic Weight24 |
| hydrogen |
1.007 94(7) |
[1.007 84; 1.008 11] |
| lithium |
6.941(2) |
[6.938; 6.997] |
| boron |
10.811(7) |
[10.806; 10.821] |
| carbon |
12.0107(8) |
[12.0096; 12.0116] |
| nitrogen |
14.0067(2) |
[14.006 43; 14.007 28] |
| oxygen |
15.9994(3) |
[15.999 03; 15.999 77] |
| silicon |
28.0855(3) |
[28.084; 28.086] |
| sulfur |
32.065(5) |
[32.059; 32.076] |
| chlorine |
35.453(2) |
[35.446; 35.457] |
| thallium |
204.3833(2) |
[204.382; 204.385] |
The most recent periodic table was
reproduced as a tear-off page on the back cover of the printed version of the March-April 2011 issue of Chemistry International. Click here for a pdf of this version of the periodic table.
In some cases, such as for trade and commerce, users may need a representative value for an element having an atomic-weight interval. Conventional atomic-weight values are conventional quantity values25 and are provided by the Commission.24 For example, the conventional atomic-weight value for hydrogen is 1.008.
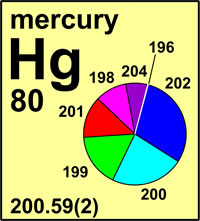
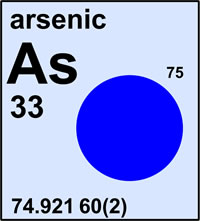
Figure 2 (below) is an example from IUPAC’s periodic table of the isotopes for the educational community.26 The isotopic abundances of an element are shown in a pie diagram. This figure shows four classifications of elements (from left to right): (a) those whose standard atomic weights are not constants of nature and that are assigned an interval, (b) those whose standard atomic weights are not constants of nature and that are not assigned an interval, (c) those whose atomic weight is a constant of nature because they have one stable isotope, and (d) those that have no standard atomic weight because they have no stable isotopes. This fundamental change in the presentation of the atomic weights represents an important advance in our knowledge of the natural world and will underscore the significance and contributions of chemistry to the well-being of humankind in the International Year of Chemistry in 2011.
 |
 |
 |
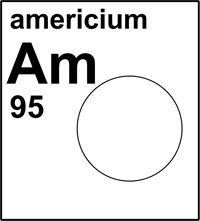 |
| Figure 2. Potential illustrations for elements in IUPAC’s new periodic table of the isotopes for the educational community26 with stable isotopic abundances shown as pie diagrams (from left to right): Element (chlorine) whose standard atomic weight is not a constant of nature and is an interval. Element (mercury) whose standard atomic weight is not a constant of nature and is not an interval. Element (arsenic) whose standard atomic weight is a constant of nature because it has one stable isotope. Element (americium) that has no stable isotopes and thus no standard atomic weight. |
Ty Coplen <[email protected]> and Norman Holden <[email protected]> are members of the IUPAC Inorganic Chemistry Division. Ty Coplen is with the U.S. Geological Survey, in Reston, Virginia, USA. Norman Holden is at the National Nuclear Data Center of the Brookhaven National Laboratory in Upton, New York.
www.ciaaw.org
Guidelines for Atomic-Weight Intervals*
- The variation in atomic-weight values, Ar(E), of an element E is termed an atomic-weight “interval” with the symbol [a; b], where a and b are the lower and upper bounds, respectively, of the interval; thus, for element E, a ≤ Ar(E) ≤ b.
- The standard atomic weight of an element, expressed as an interval, [a; b], should not be expressed as the average of a and b ± half of the difference between b and a.
- The atomic-weight interval and range should not be confused. The atomic-weight range is equal to b – a, where a and b are the lower and upper bounds, respectively.
- The lower and upper bounds commonly are determined from mass spectrometric measurements of normal materials, taking into account both the uncertainties of the measurements and the uncertainty of the “best measurement” of isotopic abundances of an element used to determine its 2007 standard atomic weight.
- The atomic-weight interval encompasses atomic-weight values of all normal materials.
- Both lower and upper bounds are consensus values, and neither has any uncertainty associated with it.
- The atomic-weight interval is the standard atomic weight, which is the best knowledge of the atomic weights of natural terrestrial sources.
- The number of significant figures in the lower and upper bounds are adjusted so that mass spectrometric measurement uncertainties do not impact the bounds.
- The number of significant figures in the lower and upper bounds should be identical. A zero as a trailing digit in a value may be needed and is acceptable.
- The atomic-weight interval is selected conservatively so that changes in the Table of Standard Atomic Weights are needed infrequently. Thus, IUPAC’s Commission on Isotopic Abundances and Atomic Weights may recommend additional conservatism and may reduce the number of significant figures.
The atomic-weight interval is given as precisely as possible and should have as many digits as possible, consistent with the previously stated rules.
- Values of atomic-weight intervals are updated in the Table of Standard Atomic Weights by the Commission following completion of an IUPAC project reviewing the published literature for peer-reviewed isotopic-abundance data.
- If the variation in isotopic composition in normal materials of an element is under evaluation by an IUPAC project, a footnote “r” may be retained in the Table of Standard Atomic Weights until the project completes its evaluation in order that changes to the tables are infrequent. Currently, such elements include He, Ni, Cu, Zn, Se, Sr, Ar, and Pb.
*See reference 24 for more details. |
References
- F.W. Clarke, “The Constants of Nature, Part 5. Recalculation of the Atomic Weights,” Smithsonian Misc. Publ. 441 i–xiv, 1–259 (1882).
- 1902 Internationale Atomgewichte, Ber. dt. chem. Ges. 35 (1902).
- www.iupac.org/reports/periodic_table/IUPAC_Periodic_Table-22Jun07b.pdf
- F. Soddy, “The Chemistry of Mesothorium.” J. Chem. Soc. 99, 72–83 (1911).
- F. Soddy, “Intra-Atomic Charge,” Nature 92, 399–400 (1913).
- J.J. Thompson. Phil. Mag. 24, 668–693 (1912).
- G.P. Baxter and J.H. Wilson. J. Am. Chem. Soc. 30, 187–195 (1908).
- F. Soddy and H. Hyman. J. Chem. Soc. 105, 1402–1408 (1914).
- T.W. Richards and M.E. Lembert. J. Am. Chem. Soc. 36, 1329–1344 (1914).
- M. Dole, “The Relative Atomic Weight of Oxygen in Water and in Air.” J. Am. Chem. Soc. 57, 2731 (1935).
- A.O. Nier and E.A. Gulbransen, “Variations in the Relative Abundances of the Carbon Isotopes,” J. Am. Chem. Soc. 61, 697–698 (1939).
- E. Wichers, J. Am. Chem. Soc. 74, 2447–2450 (1952).
- A.E. Cameron and E. Wichers, J. Am. Chem. Soc. 84, 4175–4197 (1962).
- IUPAC, Pure Appl. Chem. 21, 91–108 (1970).
- CIAAW, www.ciaaw.org/atomic_weights8.htm, as of 10 October 2010.
- N.E. Holden. Pure Appl. Chem. 52, 2349–2384 (1980).
- T.B. Coplen, J.K. Böhlke, P. De Bièvre, T. Ding, N.E. Holden, J.A. Hopple, H. R. Krouse, A. Lamberty, H.S. Peiser, K.M. Révész, S. E. Rieder, K.J.R. Rosman, E. Roth, P.D.P. Taylor, R.D. Vocke, Jr., and Y.K. Xiao. Pure Appl. Chem. 74, 1987–2017 (2002).
- T.B. Coplen, J.A. Hopple, J.K. Böhlke, H.S. Peiser, S.E. Rieder, H.R. Krouse, K.J.R. Rosman, T. Ding, R.D. Vocke, Jr., K.M. Révész, A. Lamberty, P. Taylor, and P. De Bièvre. “Compilation of Minimum and Maximum Isotope Ratios of Selected Elements in Naturally Occurring Terrestrial Materials and Reagents: U.S. Geological Survey Water-Resources Investigations Report 01-4222, 98 p (2001).
- M. Butzenlechner, A. Rossmann, and H.-L. Schmidt. J. Agric. Food Chem. 37, 410–412 (1989).
- M. Berglund and M.E. Wieser. Pure Appl. Chem. 83, 397-410 (2011) and reference 29 therein.
- H.S. Peiser, N.E. Holden, P. De Bièvre, I.L. Barnes, R. Hagemann, J.R. De Laeter, T.J. Murphy, E. Roth, M. Shima, and H.G. Thode. Pure Appl. Chem. 56, 695–768 (1984).
- N.E. Holden and R.L. Martin, Pure Appl. Chem. 55, 1101–1118 (1983).
- M.E. Wieser and M. Berglund. Pure Appl. Chem. 81, 2131–2156 (2009).
- M.E. Wieser and T.B. Coplen. Pure Appl. Chem. 83, 359–396 (2011).
- JCGM 200:2008, International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM, 3rd ed.), www.bipm.org/publications/guides/vim.html.
- www.iupac.org/web/ins/2007-038-3-200
ISSUE inside back cover - link (pdf-135KB) to the brand new updated periodic table compiled in response to the Commission’s recommendations; version date 21 January 2011 [link to collection index]
PREPRINT
-
link to the preprint version previously made available on 13 Dec 2010
> (added June 1, 2011) Tanslation from the Catalan Association of Clinical Laboratory Sciences (ACCLC, <www.acclc.cat>) Els pesos atòmics ja no són constants naturals [Art. 128] In vitro veritas 2011; volum 12, pàgs 102-110
Page
last modified 1 June 2011.
Copyright © 2003-2011 International Union of Pure and Applied Chemistry.
Questions regarding the website, please contact [email protected] |