|
|
Vol.
31 No. 2
March-April 2009
Amount of Substance and the Mole
by Ian Mills and Martin Milton
The International System of Units, the SI, is built upon seven base quantities and seven base units, as summarized in the table below. Although most of these are familiar to all scientists, the quantity “amount of substance” and its unit “mole” are less familiar and are mainly used by chemists.1 In the chemistry community, the unit “mole” is familiar, but the name of the corresponding quantity “amount of substance” is not so familiar, and the concept is still a source of difficulty for many students. This article reviews and clarifies these two concepts2 and discusses the definition of the unit “mole” and its possible revision.
| Base quantity |
symbol |
Base unit |
symbol |
| length |
l |
metre |
m |
| mass |
m |
kilogram |
kg |
| time, time interval |
t |
second |
s |
| electric current |
I, i |
ampere |
A |
thermodynamic
temperature |
T |
kelvin |
K |
| amount of substance |
n |
mole |
mol |
| luminous intensity |
Iv |
candela |
cd |
Amount of Substance
Amount of substance, symbol n, is a quantity that measures the size of an ensemble of entities. It appears in thermodynamic relations, such as the ideal gas law, and in stoichiometric relations between reacting molecules, as in the Law of Multiple Proportions. Familiar equations involving n are thus
for an ideal gas, and the equation
for the amount-of-substance concentration (usually called simply the concentration, the molar concentration, or the amount concentration) of a solution. Here, V is the volume of a solution containing the amount of solute n. Another important relation is that between amount of substance n and mass m for a pure sample
where M is the mass per amount of substance, usually called the “molar mass.” Similarly, amount concentration c (SI unit mol/dm3) may be related to mass concentration ρ (SI unit g/dm3) by the equation
An important application of the quantity n in chemistry is to the way in which molecules react in a titration (or more generally in any chemical reaction); molecules (or ions or entities) of X always react with molecules (or ions or entities) of Y in a simple ratio, such as 1:1, or 1:2, or 2:1, and so forth. This is the most fundamental concept of chemical reactions. Thus, the ratio of volumes of solutions of X and Y that react together in a titration are given by
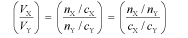 |
(5) |
where the quantity (nX/nY) is a simple rational fraction. Hence, the concentration of an unknown solution may be determined from the concentration of a standard solution by measuring the volumes in a titration. This is the law of multiple proportions.
It is difficult to give formal definitions for quantities, particularly base quantities, such as length, mass, time, temperature, and amount of substance. The most useful definitions of quantities are in terms of the equations that relate them to other quantities, and, in this way, derived quantities are defined in terms of base quantities. But defining the base quantities is more difficult. The best formal definition of “amount of substance” is as follows:
Amount of substance is a quantity proportional to the number of entities N in a sample. The proportionality constant is the same for all substances and is the reciprocal of the Avogadro constant NA.
The entities may be atoms, molecules, ions, electrons, other particles, or specified groups of such particles.
The quantity amount of substance, n, is thus an alternative to using the quantity number of entities, N. They are related by the equation
where NA is the Avogadro constant, a fundamental constant whose value is related to the unit of amount of substance n. Because the number of entities N is a dimensionless number, the dimension of NA is the reciprocal of the dimension of n and is thus (amount of substance)-1.
One might reasonably ask why we need the quantity amount of substance n at all. Why not simply use number of entities N in its place? There are three reasons for preferring the use of n rather than N:
- First, equations, such as Equation 3, can be used to determine molar mass M, or amounts in terms of moles, without knowing the value of the Avogadro constant. The atomic weights of atoms in the periodic table were known long before the value of the Avogadro constant was known with similar accuracy. Even today, the value of the Avogadro constant is known only to about a part in 107, whereas many atomic weights are known to about a part in 109 or better.
- A second reason is practical: The number of entities is generally of the order 1023, whereas n is generally a number of order 1 when expressed in moles. Thus, for example, in a chemistry laboratory, the concentration of solutions is typically quoted in moles per litre, with numbers in the general order of magnitude 1. It would be inconvenient to quote concentrations in molecules per litre, with numbers of the order 1023. Thus we find bottles labeled “0.1 M NaOH,” where M is read as “molar” and is an accepted shorthand for the unit mol/L = mol/dm3. The quantity amount of substance may be seen as a device used to handle the same quantitative information with much smaller numbers.
- A third motivation for introducing the quantity amount of substance with the mole as a base unit is that it extends the power of dimensional analysis in chemistry, and to equations involving chemical quantities. This follows from the fact that n is a base quantity with its own dimension, whereas N is dimensionless.
The Mole
The mole, with symbol mol, is the SI unit for the quantity amount of substance. It is currently defined as follows:3
The mole is that amount of substance that contains the same number of elementary entities as there are atoms in 12 g of carbon 12. When the mole is used, the entities must be specified and may be atoms, molecules, ions, electrons, other particles, or specified groups of such particles.
It follows that the numerical value of the Avogadro constant, denoted {NA}, expressed in the unit mol-1, is simply the number of atoms in 12 g of carbon 12, so that the value of the Avogadro constant is directly related to the definition of the mole. The present best estimate of the Avogadro constant is4
| NA = 6.022 141 79 (30) x 1023 mol-1 [ur = 5 x 10-8] |
(7) |
where the number in square brackets is the relative standard uncertainty.
The effect of this definition is that the molar mass of carbon 12, M(12C), is exactly 12 g/mol, and the molar mass of any atom or molecule X is determined from its atomic or molecular weight by simply multiplying by the unit g/mol, without the need to know the value of the Avogadro constant. This is summarized in the relations
| M(12C) = Ar(12C) g/mol = 12 g/mol |
(8) |
| M(X) = Ar(X) g/mol |
(9) |
Here, Ar(X) is the recommended symbol for the molecular weight of the entity X. The atomic or molecular weight of an entity is actually the relative atomic or molecular mass, relative to the value for the carbon 12 atom taken as exactly 12. The names “atomic weight” and “molecular weight” are universally used and have been officially sanctioned by IUPAC, although they are actually dimensionless quantities and are not either masses or weights.
The Names “Mole” and “Amount Of Substance”
The name “mole” has been—and still is—the cause of some confusion. Its origin has been discussed in several publications.5 The terms “Kilogrammemolekuel” and “g-Molekel” were used by German scientists in the 1880s and 1890s. The term “gramme-molecule” was first used in English in 1893 in an article in the Encyclopedia Britannica. As the term implies, one gram molecular weight of a substance X is that amount in a mass equal to the molecular weight expressed in grams.
These terms proved too awkward for everyday use, and the shortening of the term “g-Molekel” to “Mol” was first recorded in 1898 by Nernst.6 The term “mole” appears in English for the first time in the translation of Ostwald’s Principles of Inorganic Chemistry, published in 1902, in which Ostwald associated the term with a standard number of molecules. Thus, one gram molecule of X became one mole of X.
The development of mass spectrometry and the discovery of isotopes in the early twentieth century led to the transition of atomic weights from a basis of either 16 for the naturally occurring mix of oxygen isotopes (used in chemistry) or 16 for the 16O isotope (used in physics), and eventually to the use of 12 for 12C, adopted in 1961 and described as the “unified atomic mass scale.” During this period, it was recognized that the quantity for which the mole was a unit itself deserved recognition as a quantity, and it was given the name “amount of substance.” The International Committee for Weights and Measures (Comité International des Poids et Mesures, CIPM), with the support of IUPAC, the International Union of Pure and Applied Physics (IUPAP), and the International Organization for Standardization (ISO), adopted “amount of substance” as a base quantity and “mole” as a base unit in 1971.7
It must be admitted that the name “amount of substance” is not well chosen; the word “amount” has a common dictionary meaning, and the additional words “of substance” seem inadequate to imply chemists’ more special meaning for this name. It was the original intention that the words “of substance” should be replaced by the specification of the entity whenever possible, so that one would say (for example) “amount of benzene, C6H6” or “amount of hydrogen ions, H+.” Note the importance of specifying the molecular formula of the entity. For example, “amount of sulphur” might refer to an entity S, or S2, or S8 without further specification of the molecular formula. Yet in practice, many people say “amount of substance of benzene,” or even “amount of substance of substance benzene,” which is long winded and seems like a tautology in addition to being ambiguous.
Other names have been suggested for the quantity n. A possible name might be “chemical amount,” because this quantity has to do with chemistry. The name “chemical amount” for n would then naturally extend to the name “chemical concentration” for c (compare with the name “mass concentration” for C), and when there is no confusion, the adjective “chemical” might be dropped—leading to the names that are usually used today in such phrases as “an amount of three moles,” or “a concentration of 0.1 mol/dm3.” The name “enplethy” has also been suggested for amount of substance; see the discussion on page 4 of the new edition of the IUPAC Green Book.8
Another name for n, which is the name that most chemists use, is simply “number of moles.” However, this name is problematic because it confuses the name of the quantity with the name of the unit. For this reason, we would not regard “number of kilograms” as an acceptable synonym for “mass” nor “number of kelvins” as an acceptable synonym for “temperature.” A clear understanding requires that we always distinguish between quantities and units. Thus, mass is a quantity, for which kilogram (or gram, or milligram) is a unit; similarly, we wish to say that amount of substance is a quantity, for which mole (or millimole, or micromole) is a unit.
Setting aside the difficulties with the name “amount of substance,” it is important to realize that in the system of quantities and units that is now universally adopted in chemistry, amount of substance n is regarded as a base quantity with its own dimension, whereas—in contrast—number of entities N is regarded as a dimensionless quantity.
A Possible New Definition for the Mole
The current definition of the seven base units of the SI is given in the SI Brochure.3 However, proposals are under discussion to adopt new definitions for four of the base units. This follows from our desire to define each of the base units in relation to one of the fundamental constants of physics, or the properties of a simple atom, because we believe these to be the most stable and reliable constants of nature available. Specifically, new definitions are being considered for the kilogram, ampere, kelvin, and mole. This is the subject known as quantum metrology, and the proposals are discussed in detail elsewhere.9 However, the proposed new definition of the mole is particularly relevant to this discussion, and the suggestion is that it should simply specify the number of entities in a mole. This new definition might then read as follows:
The mole is that amount of substance of a
system that contains exactly 6.022 141 79 x 1023 specified elementary entities, which may be atoms, molecules, ions, electrons, other particles, or specified groups of such particles.
The effect of this new definition would be to fix the value of the Avogadro constant to be 6.022 141 79 x 1023 mol-1 exactly. The number would be chosen to be the best estimate of the numerical value of the Avogadro constant at the time the new definition is adopted, thus ensuring continuity in the value of the mole.
This new definition would be conceptually simpler than the current definition, which is chosen to fix the molar mass of carbon 12 rather than the number of entities in a mole. Also, the new definition would no longer be dependent on the kilogram, so that uncertainties in realizing the definition of the kilogram would no longer be transmitted to the mole, as they are at present.
The Molar Mass Constant Mu
Many of the relations between the quantities discussed here can be simplified by introducing the molar mass constant Mu, defined as one twelfth of the molar mass of the carbon 12 atom. This is the natural analog on the macroscopic scale of the unified atomic mass constant mu on the atomic scale, defined as one-twelfth of the mass of a carbon 12 atom. The quantity mu is often used as a unit of atomic mass, denoted either u (for “unified”) or Da (for “dalton,” a name for this unit that is widely used in the biosciences for expressing the mass of biomolecules with many thousands of atoms). Thus, we have
| Mu = M(12C) / 12 |
(10) |
| and |
|
| mu = m(12C) / 12 = 1 u = 1 Da |
(11) |
The molar mass M(X) of any entity X is then given in terms of the molecular weight Ar(X) by the equation
| M(X) = Ar(X) Mu |
(12) |
| just as the atomic mass of the entity X is given by |
|
| m(X) = Ar(X) mu |
(13) |
In the current SI, Mu = 1 g/mol exactly, and the Avogadro constant is an experimentally determined quantity (the number of atoms in 12 g of carbon 12), whose value is currently known with a relative standard uncertainty of about 5 x 10-8 (CODATA 2006). With the new definition proposed above, Mu will initially have the same value of 1 g/mol, but it will be an experimentally determined quantity with an uncertainty, and its value may change slightly from 1 g/mol as a result of future adjustments in the values of other constants. However, the relative change of Mu from the value 1 g/mol is unlikely ever to be greater than a few parts in 109, and this is so much smaller than the uncertainty with which chemical measurements are likely to be made that for all practical purposes, chemists may still treat Mu as being equal to 1 g/mol.
The relation between the Avogadro constant and the Planck constant presented by Mohr and Taylor,4 which follows from the theoretical expression for the Rydberg constant R∞, remains true under both the current and new definition of the mole:
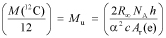 |
(14) |
In this equation, α is the fine structure constant, c is the speed of light in a vacuum, h is the Planck constant, and Ar(e) is the relative mass of the electron on the unified atomic mass scale.
The molar mass constant Mu has not been much used in the established literature. It can, of course, always be replaced by the expression M(12C)/12, which is how it is defined. We believe that this constant could be used to greater advantage than it is at present—in teaching chemistry, for example, to simplify the expression for calculating the molar mass of atoms and molecules.
Summary and Acknowledgements
It is something of a paradox that such concepts as the quantity “amount of substance” and its unit “mole,” so widely used by practical chemists, are also the subjects of widespread misunderstanding. The proposed new definition for the mole would simplify the link between the mole and the Avogadro constant, which has its own long and rich history.
This short article owes much to a paper drafted by B.N. Taylor for the benefit of the Consultative Committee for Units meeting held in June 2007. We are also grateful to Fabienne Meyers for a number of suggestions that improved this manuscript.
References
1. The quantity “luminous intensity” and its unit “candela” are also used only by a specialized community, but these quantities are not discussed here.
2. Guggenheim discussed these concepts in a short paper written nearly 50 years ago (E.A.Guggenheim, J. Chem. Ed. 1961, 38, 86–87).
3. The International System of Units (the SI Brochure), 8th ed., International Bureau of Weights and Measures, 2006. ISBN 92-822-2213-6.
4. Mohr, P.J., B.N. Taylor, and D.B. Newell, Rev. Mod. Phys. 2008, 80(2), 633–730, or J. Phys. Chem. Ref. Data 2008, 37(3), 1187–1284.
5. Cerruti, L. “The Mole, Amedeo Avogadro, and Others.” Metrologia, 1994, 31, 159–166; McGlashan, M.L. “Amount of Substance and the Mole.” Metrologia, 1994/95, 31, 447–455.
6. Nernst, W. Theoretische Chemie von Standpunkte der Avogadroschen Regel und der Thermodynamic, 1898.
7. 14th CGPM 1971, Resolution 3, and Metrologia 1972, 8, 36.
8. Quantities, Units and Symbols in Physical Chemistry, 3rd ed., RSC Publishing for IUPAC, 2007.
9. Mills et al. “Redefinition of the Kilogram, Ampere, Kelvin and Mole: A Proposed Approach to Implementing CIPM Recommendation 1 (CI-2005),” Metrologia 2006, 43, 227–246.
Ian Mills <[email protected]> is a professor at the School of Chemistry, University of Reading, Reading, UK. Martin Milton <[email protected]> is a science fellow at the National Physical Laboratory, Hampton Road, Teddington, UK.
Page
last modified 4 March 2009.
Copyright © 2003-2009 International Union of Pure and Applied Chemistry.
Questions regarding the website, please contact [email protected] |